Understanding Reactance: A Deep Dive into Inductive and Capacitive Properties
Many who have ventured into the realm of electrical engineering are likely familiar with the concept of reactance, especially its two fundamental equations used to compute both inductive and capacitive reactance. However, unless one has thoroughly explored this topic, their understanding may be superficialakin to how a student memorizes the formula for the area of a circle without grasping the underlying principles of geometry. To delve deeper into the essence of these equations, a seasoned electrical engineer, known in the community as [Old Hack EE], took the initiative to investigate and share his findings through an engaging video presentation.
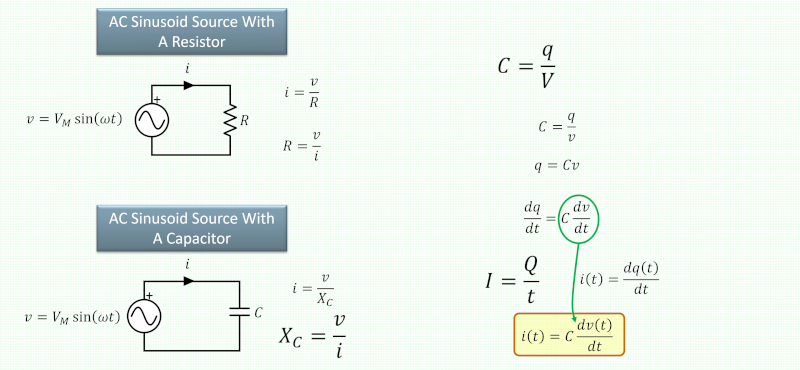
The core idea behind understanding reactance is relatively straightforward: it describes the relationship between voltage and current flowing through a reactive component, much like resistance does. However, reactance is distinctly different from resistance in that it is not merely a fixed value; instead, it represents a variable curve that changes at different frequencies. This variability arises because, in reactive components, the current and voltage are out of phase, complicating the straightforward calculation.
For those with a background in calculus, the explanations presented in [Old Hack EE]'s video will resonate well. Conversely, viewers who may not be well-versed in calculus might initially feel overwhelmed, but fear notunderstanding is still within reach. A crucial aspect of these equations lies in interpreting frequency measured in Hertz (Hz) as cycles per second. The presence of 2 in these equations serves as a bridge to transitioning from frequency to what is known as radian frequency. This is vital since one complete cycle per second corresponds to a 360-degree rotation of a sine wave within that same timeframe. With 2 radians completing a full circle, this relationship makes logical sense.
This exploration into reactance highlights the beauty of developing intuition around concepts that, despite appearing fundamental, possess a depth often overlooked in academia. For those seeking a refresher or an introduction to calculus, it is worth noting that it is not as daunting as it may seem at first glance. Engineers frequently utilize advanced mathematical tools such as vectors or imaginary numbers to effectively analyze and work with reactance. For those interested in expanding their knowledge further, resources on these advanced topics are also available.